AI giải quyết vấn đề (Phần 1)

I. Tìm kiếm và giải quyết vấn đề

Nhiều vấn đề có thể được diễn giải như vấn đề tìm kiếm. Điều này đòi hỏi chúng ta phải bắt đầu bằng cách hình thành các lựa chọn thay thế và hậu quả của chúng.

Tìm kiếm trong thực tế: đi từ A đến B
Hãy tưởng tượng bạn đang ở một thành phố nước ngoài, tại một địa chỉ nào đó (chẳng hạn như một khách sạn) và muốn sử dụng phương tiện công cộng để đến một địa chỉ khác (có lẽ là một nhà hàng đẹp). Bạn làm thế nào? Nếu giống như nhiều người, bạn rút điện thoại thông minh ra, gõ điểm đến và bắt đầu làm theo hướng dẫn.

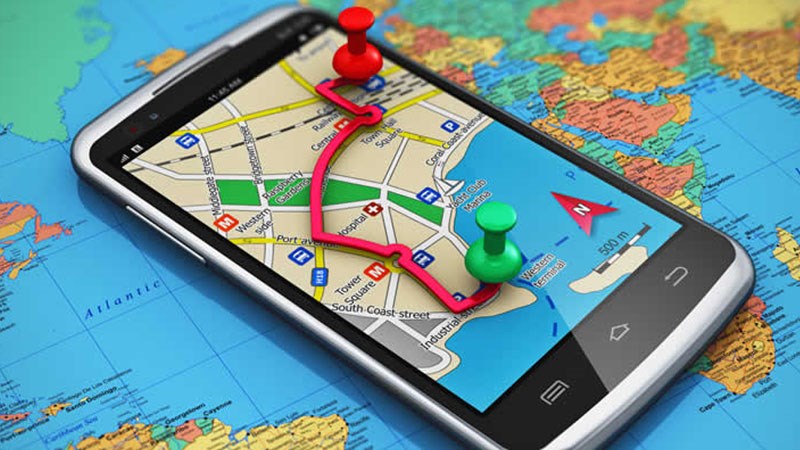
Câu hỏi này thuộc về lớp các bài toán tìm kiếm và lập kế hoạch. Các vấn đề tương tự cần được giải quyết bằng xe tự lái và AI để chơi game. Ví dụ, trong trò chơi cờ vua, khó khăn trong việc giành được quân từ A đến B là giữ an toàn cho quân của bạn trước đối thủ.

Thường thì có nhiều cách khác nhau để giải quyết vấn đề, một số cách trong số đó có thể phù hợp hơn về thời gian, công sức, chi phí hoặc các tiêu chí khác. Các kỹ thuật tìm kiếm khác nhau có thể dẫn đến các giải pháp khác nhau và việc phát triển các thuật toán tìm kiếm nâng cao là một lĩnh vực nghiên cứu được thiết lập.

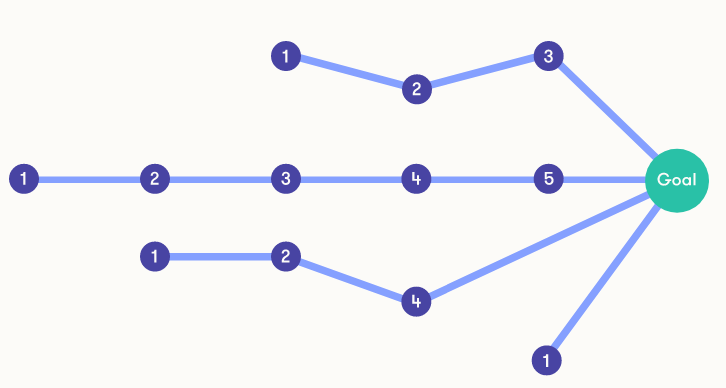
chúng ta sẽ không tập trung vào các thuật toán tìm kiếm thực tế. Thay vào đó, chúng tôi nhấn mạnh giai đoạn đầu tiên của quá trình giải quyết vấn đề: xác định các lựa chọn và hệ quả của chúng, điều này thường không tầm thường và có thể đòi hỏi sự suy nghĩ cẩn thận. Chúng ta cũng cần xác định rõ mục tiêu của mình là gì, hay nói cách khác, khi nào chúng ta có thể coi vấn đề đã được giải quyết. Sau khi điều này được thực hiện, chúng ta có thể tìm kiếm một chuỗi các hành động dẫn từ trạng thái ban đầu đến mục tiêu.

chúng ta sẽ thảo luận về hai loại vấn đề:

• Tìm kiếm và lập kế hoạch trong môi trường tĩnh chỉ với một “đối tượng”
• Trò chơi có hai người chơi (“đối tượng”) thi đấu với nhau

Các danh mục này không bao gồm tất cả các tình huống có thể xảy ra trong thế giới thực, nhưng chúng đủ chung để thể hiện các khái niệm và kỹ thuật chính.

Trước khi giải quyết các tác vụ tìm kiếm phức tạp như điều hướng hoặc chơi cờ vua, chúng ta hãy bắt đầu từ một mô hình đã được đơn giản hóa nhiều để nâng cao hiểu biết về cách chúng ta có thể giải quyết vấn đề bằng AI.

Bài toán trò chơi: gà qua sông

Chúng ta sẽ bắt đầu từ một câu đố đơn giản để minh họa các ý tưởng. Một robot trên thuyền cần di chuyển ba vật qua sông: một con cáo, một con gà và một bao tải thức ăn cho gà. Cáo sẽ ăn thịt gà nếu nó có cơ hội, và gà sẽ ăn thức ăn của gà nếu nó có cơ hội, và cả hai đều không phải là kết quả mong muốn. Robot có khả năng giữ cho động vật không gây hại khi ở gần chúng, nhưng chỉ có robot mới có thể vận hành chèo thuyền và chỉ có hai trong số các vật có trên thuyền cùng với robot. Làm thế nào mà robot có thể di chuyển tất cả hàng hóa của nó sang bờ sông đối diện?

Chúng tôi sẽ mô hình câu đố bằng cách lưu ý rằng năm thứ có thể di chuyển được đã được xác định: rô bốt, thuyền, cáo, gà và thức ăn cho gà. Về nguyên tắc, mỗi người trong số năm người có thể ở hai bên sông, nhưng vì chỉ có robot mới có thể vận hành thuyền chèo nên cả hai sẽ luôn ở cùng một phía. Do đó, có bốn thứ với hai vị trí có thể có cho 1 trường hợp, tạo nên mười sáu sự tổ hợp, mà chúng ta sẽ gọi là trạng thái:

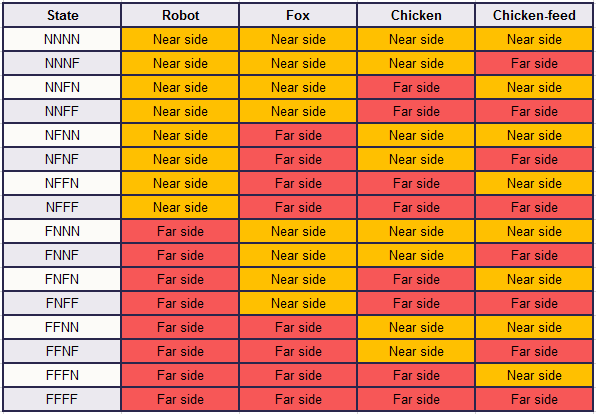
Chúng ta đã đặt tên ngắn gọn cho các trạng thái,”ở phía gần – vị trí ban đầu” là “N”,”ở phía xa – sang bên sông” là “F”. Bây giờ chúng ta có trạng thái ban đầu là NNNN và trạng thái mục tiêu là FFFF, thay cho nói “ở trạng thái ban đầu, rô-bốt ở phía gần, cáo ở phía gần-ban đầu, gà ở phía gần-ban đầu , và cả thức ăn cho gà ở phía gần-ban đầu, và trong trạng thái mục tiêu, robot ở phía xa-sang sông ”, v.v.

Một số trạng thái bị cấm bởi các điều kiện giải đố. Ví dụ, ở trạng thái NFFN (nghĩa là robot ở phía gần với thức ăn cho gà nhưng cáo và gà ở phía xa), cáo sẽ ăn gà, điều mà chúng ta không thể có. Vì vậy, chúng tôi có thể loại trừ các trạng thái NFFN, NFFF, FNNF, FNNN, NNFF và FFNN (bạn có thể kiểm tra từng trạng thái nếu bạn nghi ngờ lý do của chúng tôi). Chúng tôi còn lại với mười trạng thái sau:

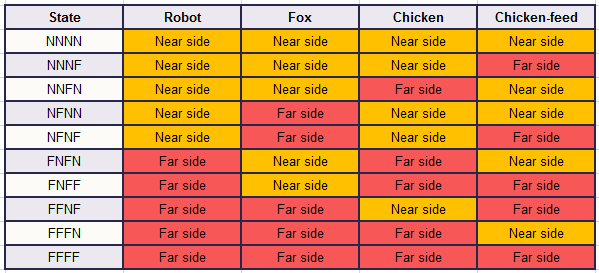
Tiếp theo, chúng ta sẽ tìm hiểu xem có thể chuyển đổi trạng thái nào, nghĩa là đơn giản là khi robot xếp con thuyền với một số vật phẩm là hàng hóa, trạng thái kết quả sẽ như thế nào trong mỗi trường hợp. Tốt nhất là vẽ một sơ đồ của các quá trình chuyển đổi, và vì trong bất kỳ quá trình chuyển đổi nào, chữ cái đầu tiên sẽ xen kẽ giữa N và F, rất thuận tiện để vẽ các trạng thái bắt đầu bằng N (vì vậy robot ở phía gần) trong một hàng và các trạng thái bắt đầu bằng F trong một hàng khác:

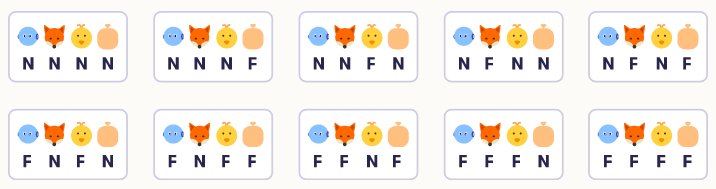
Bây giờ chúng ta hãy vẽ các chuyển tiếp. Chúng ta có thể vẽ các mũi tên có hướng để chúng hướng từ nút này sang nút khác, nhưng trong câu đố này, quá trình chuyển đổi là đối xứng: nếu rô bốt có thể chuyển từ trạng thái NNNN sang trạng thái FNFF, nó cũng có thể chuyển theo cách khác từ FNFF đến NNNN. Vì vậy, đơn giản hơn là vẽ các chuyển đổi đơn giản với các đường không có hướng. Bắt đầu từ NNNN, chúng ta có thể chuyển đến FNFN, FNFF, FFNF và FFFN:

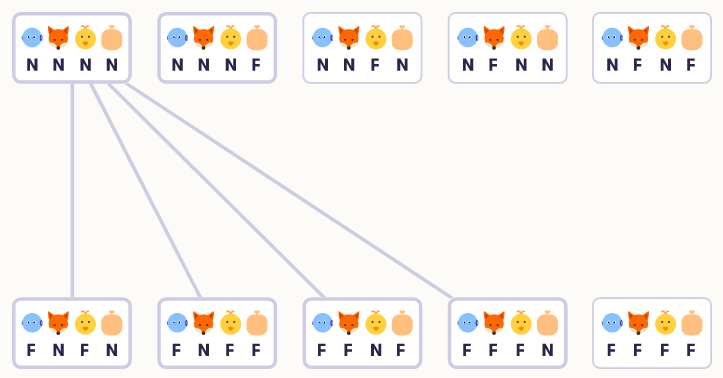
Sau đó, chúng ta điền vào phần còn lại:

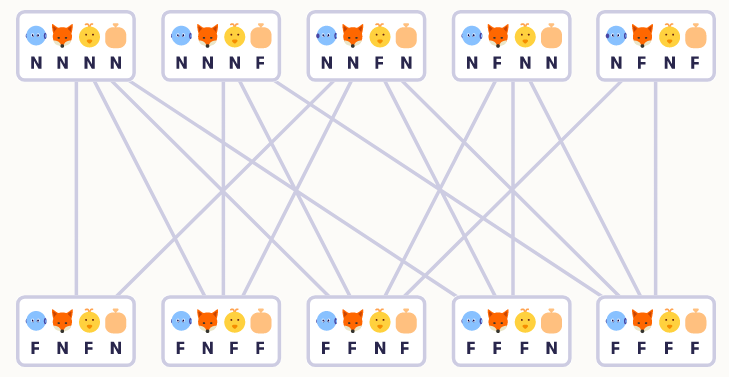
Bây giờ chúng tôi đã thực hiện khá nhiều công việc trên câu đố mà không có vẻ gần hơn với lời giải, và có một chút nghi ngờ rằng bạn có thể đã giải được toàn bộ câu đố bằng cách sử dụng “trí thông minh tự nhiên” của mình. Nhưng đối với những vấn đề phức tạp hơn, trong đó số lượng các giải pháp khả thi tăng lên hàng nghìn và hàng triệu, cách tiếp cận hệ thống hoặc máy móc của chúng tôi sẽ tỏa sáng vì phần khó sẽ phù hợp với một máy tính đơn giản. Bây giờ chúng ta đã hình thành các trạng thái thay thế và chuyển tiếp giữa chúng, phần còn lại trở thành một nhiệm vụ cơ học: tìm đường đi từ trạng thái ban đầu NNNN đến trạng thái cuối cùng FFFF.

Một trong những con đường như vậy được tô màu trong hình sau. Đường đi từ NNNN đến FFFN (rô bốt đưa cáo và gà sang phía bên kia), sau đó đến NFNN (rô bốt đưa gà trở lại phía xuất phát) và cuối cùng là FFFF (rô bốt hiện có thể di chuyển gà và cho gà ăn sang phía bên kia).

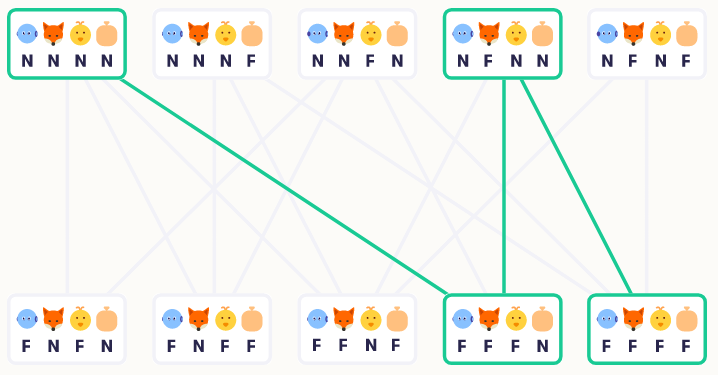
Không gian trạng thái, quá trình chuyển đổi và chi phí
Để chính thức hóa một vấn đề quy hoạch, chúng tôi sử dụng các khái niệm như không gian trạng thái, quá trình chuyển đổi và chi phí.

Thuật ngữ chính

Không gian trạng thái
có nghĩa là tập hợp các tình huống có thể xảy ra. Trong câu đố vượt gà, không gian trạng thái bao gồm mười trạng thái được phép từ NNNN đến FFFF (nhưng không phải NFFF, ví dụ như NFFF mà các quy tắc câu đố không cho phép). Nếu nhiệm vụ là điều hướng từ địa điểm A đến địa điểm B, không gian trạng thái có thể là tập hợp các vị trí được xác định bởi tọa độ (x, y) của chúng có thể đạt được từ điểm xuất phát A. Hoặc chúng ta có thể sử dụng một tập hợp các vị trí bị ràng buộc , ví dụ, các địa chỉ đường phố khác nhau để số lượng các tiểu bang có thể bị hạn chế.

Chuyển tiếp
là các chuyển động có thể có giữa trạng thái này và trạng thái khác, chẳng hạn như NNNN sang FNFN. Điều quan trọng cần lưu ý là chúng tôi chỉ tính các chuyển đổi trực tiếp có thể được thực hiện bằng một hành động duy nhất là chuyển tiếp. Một chuỗi gồm nhiều chuyển đổi, ví dụ, từ A sang C, từ C sang D và từ D sang B (mục tiêu), là một con đường chứ không phải là một quá trình chuyển đổi.

Chi phí
đề cập đến thực tế rằng, đôi khi các quá trình chuyển đổi khác nhau không giống nhau. Chúng có thể khác nhau về cách làm cho một số chuyển đổi thích hợp hơn hoặc rẻ hơn (theo nghĩa không nhất thiết là tiền tệ của từ này) và những chuyển đổi khác tốn kém hơn. Chúng ta có thể thể hiện điều này bằng cách liên kết với mỗi lần chuyển đổi một chi phí nhất định. Nếu mục tiêu là giảm thiểu tổng quãng đường di chuyển, thì chi phí tự nhiên là khoảng cách địa lý giữa các trạng thái. Mặt khác, mục tiêu thực sự có thể là giảm thiểu thời gian thay vì khoảng cách, trong trường hợp đó, chi phí tự nhiên rõ ràng sẽ là thời gian. Nếu tất cả các chuyển đổi đều bằng nhau, thì chúng ta có thể bỏ qua các chi phí.

Bài tập 1:  Sử dụng một chiếc thuyền nhỏ hơn trong câu đố này, robot chỉ có thể xếp một thứ trên thuyền với nó. Không gian trạng thái vẫn như cũ, nhưng có thể có ít quá trình chuyển đổi hơn.

Sử dụng sơ đồ với các trạng thái có thể có dưới đây làm điểm bắt đầu, vẽ các chuyển đổi có thể có trong đó (thực hiện điều này bằng bút chì và giấy dễ dàng hơn RẤT NHIỀU).Sau khi vẽ sơ đồ chuyển đổi trạng thái, hãy tìm đường đi ngắn nhất từ NNNN đến FFFF và tính số lần chuyển đổi trên đó. Gợi ý: Không đếm số lượng trạng thái, nhưng số lượng chuyển đổi. Ví dụ, số lượng chuyển tiếp trong đường dẫn NNNN → FFNF → NFNF → FFFF là 3 thay vì 4.

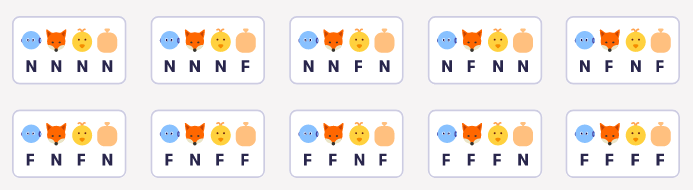
(còn tiếp)